
This paper analyses the effects of altruism on the formation of climate coalitions in the standard two-stage game of self-enforcing international environmental agreements with identical countries. Altruism implies that each country values, to some extent, every other country’s welfare when deciding on its coalition membership and emissions policy. In the Nash [Stackelberg] game, the fringe [coalition] countries exploit the altruism of the coalition [fringe] countries so that altruism decreases [increases] the coalition size. In any case, global emissions and global welfare are close to the non-cooperative values. However, altruism narrows the gap between the individually optimal emissions and the socially optimal emissions, so altruism increases global welfare. The effects of altruism on the formation of climate coalitions crucially depends on its modelling: If altruism affects the membership decision but not the policy decision, or if each coalition country is more altruistic toward other coalition countries than toward fringe countries, altruism can stabilise large coalitions up to the grand coalition. Finally, altruism can stabilise small coalitions but destabilises large coalitions with asymmetric countries.

Avoid common mistakes on your manuscript.
The Paris Agreement, negotiated by 196 parties at the 2015 United Nations Climate Change Conference, aims to limit global warming to well below 2 °C compared to pre-industrial levels (UN 2015). Although there is thus broad consensus on the international goal of climate policy, a continuation of current policies would result in global warming of about 3 °C above pre-industrial levels (UN 2023). Footnote 1 Consequently, the Paris Agreement with its nationally determined contributions does not constitute an effective international environmental agreement in terms of the international political narrative. On the other hand, some world regions have introduced rather high carbon prices despite facing negative social costs of carbon (see Table 1). Although these carbon prices are still well below the global social cost of carbon (418/tCO2 from Ricke et al. 2018), this behaviour can hardly be explained with perfect selfishness. Footnote 2
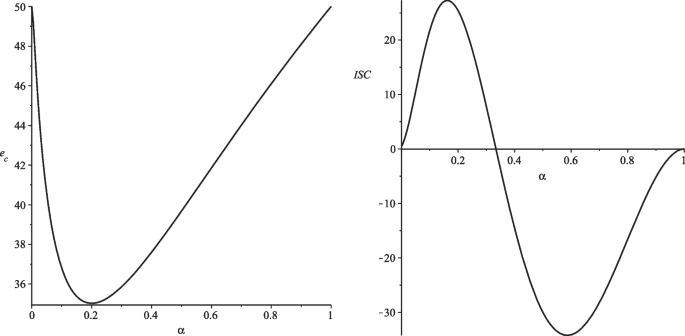
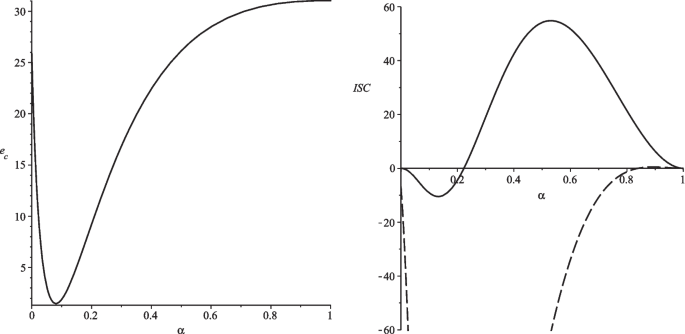
We use a numerical example to demonstrate that there are economies in which \(m=2\) is not stable for \(\alpha >0\) and \(n\ge 12\) . Figure 1 depicts each coalition country’s minimal emissions Footnote 15 (left-hand side figure) and the internal stability condition for \(m=2\) (right-hand side figure) dependent on \(\alpha\) . In the numerical example, each coalition country’s emissions are positive for all \(m\in [2,n]\) . Furthermore, \(m=2\) becomes unstable for \(\alpha \ge 0.334\) . Thus, there are economies in which \(m=2\) is not stable for \(\alpha >0\) and \(n\ge 12\) .
The third bullet of Proposition 2 and Fig. 1 show that altruism does not stabilise larger coalitions, but even destabilises small coalitions. This is in stark contrast to the numerical analysis of van der Pol et al. (2012), who find that the coalition size increases with the altruism parameter and that the grand coalition becomes stable for \(\alpha \ge 0.401\) (without community altruism and transfers). The major difference between their model and our model is that we assume altruistic preferences at both stages of the game, while they assume altruistic preferences only at the first stage of the game. At the second stage of the game, they assume that each fringe country maximizes its material welfare, while each coalition country maximizes the sum of the coalition countries’ material welfare. Footnote 16 This does not alter the qualitative results at the second stage of the game, i.e. Proposition 1 and the first bullet of Lemma 1 also hold for \(\alpha =0\) . However, it alters the qualitative effects of altruism on the internal stability condition. In both models, this internal stability condition reads
$$\begin
In van der Pol et al. (2012), where the policy is independent of \(\alpha\) , altruism stabilises coalitions if and only if
This direct effect of altruism is positive if and only if the total material welfare of the other countries decreases when a country leaves the coalition. Then, altruism can induce a country to stay in the coalition even though its own material welfare would increase if it left the coalition. In Appendix A.2.4, we prove that the direct effect is positive for \(m=2\) (and for \(m\in [2,n]\) with specification (9)), regardless of whether or not altruistic preferences are assumed at the second stage of the game. However, the magnitude of the direct effect differs between the models. Furthermore, in our model, where the policy depends on \(\alpha\) , altruism stabilises coalitions if and only if
The second line of (12) represents the indirect effect of altruism. It is positive if and only if the policy effect of altruism on a country’s moral welfare is greater inside than outside the coalition. In Appendix A.2.4, we prove that the policy effect inside the coalition is positive, i.e. \((1-\alpha )\frac>W_c(m)>>\alpha >+\alpha \frac>W(m)>>\alpha >>0\) , but that the policy effect outside the coalition is also positive for \(m=2\) (and for \(m\in [2,n-2]\) with specification (9)), i.e. \((1-\alpha )\frac>W_f(m-1)>>\alpha >+\alpha \frac>W(m-1)>>\alpha >>0\) . Proposition 2 reveals that the latter effect is so strong that altruism raises the free-rider incentives. In other words, the policy effect of altruism is more important for small coalitions than for large coalitions, and so important that the negative indirect effect of altruism outweighs the positive direct effect.
In order to check whether the different results of van der Pol et al. (2012) indeed stem from the different assumption concerning altruistic preferences at the second stage of the game, and not from some other minor differences between the models, we analyse the first stage of the game without altruistic preferences at the second stage of the game. In Appendix A.2.5, we then prove
(Stability of coalitions without policy altruism) Consider specification (9) and suppose altruism affects the membership decision but not the policy decision.
The first bullet of the proposition reveals that there is at most one stable coalition size. The second bullet of Proposition 3 mirrors the second bullet of Proposition 2, since the models with and without altruistic preferences at the second stage of the game coincide for \(\alpha =0\) . The rest of Proposition 3 confirms the numerical result of van der Pol et al. (2012) that considering altruism only at the first stage of the game stabilises coalitions. In particular, the grand coalition becomes stable when the altruism parameter is greater than a critical value, which lies between 3/7 and 4/7 for \(n\ge 12\) and \(d\le >\) .
At the second stage of the Stackelberg game, each fringe country \(i=f\) maximizes its moral welfare (1) over its emissions \(e_f\) , taking the other countries’ emissions as given, which yields (4).
Furthermore, each coalition country \(i=c\) maximizes the sum of the coalition countries’ moral welfare (3) over its emissions \(e_c\) , taking the other coalition countries’ emissions as given, but taking (4) into account, which yields Footnote 18
$$\beginwhere \(R'_f\in (-1,0)\) from (6). For \(\alpha =0\) , each coalition country equates marginal emissions benefits to the coalition countries’ marginal emissions damages \(mD'(e)\) , corrected for the leakage rate to the fringe countries \(\big |R'_f\big |\) . For \(\alpha >0\) , altruism implies that each coalition country accounts for all other countries’ marginal emissions damages via \(1+\alpha (n-1)\) , but it also implies that all other coalition countries account for each coalition country’s marginal emissions benefits via \(1+\alpha (m-1)\) . Furthermore, altruism implies that each coalition country accounts for all fringe countries’ marginal emissions benefits, which reduces the influence of the leakage rate to the fringe countries via \(1-\alpha\) . Finally, altruism of the fringe countries implies that these countries react more sensitive to other countries’ emissions changes, such that the altruism parameter ceteris paribus increases the leakage rate to the fringe countries. Note that \(B'(e_f)=B'(e_c)=nD'(e)\) for \(\alpha =1\) , so the Stackelberg equilibrium and the social optimum then coincide. In the following we focus on \(\alpha \in [0,1)\) .
From (4) and (13), we infer
$$\beginConsequently, each fringe country’s emissions are greater [smaller] than each coalition country’s emissions for \(\tilde>[<]1\) . Furthermore, \(\tilde=1\) implies that the Stackelberg equilibrium and the BAU coincide. In Appendix A.3.2, we prove Footnote 19
(Comparison of Stackelberg equilibrium and BAU)
The partial derivative of \(\tilde\) with respect to m is positive, so the coalition countries tend to become more ambitious as the coalition gets larger. Then, the leakage rate to the fringe countries ceteris paribus becomes smaller, which tends to increase \(\tilde\) , see (6). Furthermore, the coalition countries’ marginal emissions damages then become greater, which outweighs the greater coalition countries’ marginal emissions benefits and increases \(\tilde\) , see (14). In Appendix A.3.3, we prove Footnote 20
(Relation between coalition size and coalition’s ambition) Suppose \(B'''\ge 0\) and \(D'''\le 0\) . Then, \(m\lesseqgtr >\Longleftrightarrow \tilde\lesseqgtr 1\) , where
$$\beginThus, the coalition countries are less [more] ambitious than the fringe countries in small [large] coalitions, in which the leakage effect outweighs [is outweighed by] the marginal emissions damage effect. The partial derivative of \(>\) with respect to \(\alpha\) is positive, so the respective threshold coalition \(>\) tends to get larger as countries become more altruistic. In other words, the coalition countries tend to become less ambitious in the fight against climate change compared to the fringe countries. On the one hand, the altruism parameter ceteris paribus increases the importance of all other coalition countries’ marginal emissions benefits for the optimal policy, and it increases the leakage rate to the fringe countries. On the other hand, it ceteris paribus increases the importance of all fringe countries’ marginal emissions benefits for the optimal policy. Proposition 5 reveals that the former effect outweighs the latter with linear-quadratic consumption benefits.
Since \(m\ge >\) will turn out to be the relevant coalition size and to prepare the analysis of the first stage of the Stackelberg game, we prove in Appendix A.3.4 Footnote 21
(Effects of coalition size and altruism on emissions and welfare for \(m\ge >\) ) Suppose \(B'''\ge 0\) and \(D'''\le 0\) .
From the first bullet of the lemma, we get the typical results that each fringe country’s emissions increase but global emissions decrease with the coalition size, so free-rider incentives tend to increase as the coalition gets larger as in the Nash game. Contrary to the Nash game, the resulting lower climate damages ensure that not only each fringe country’s moral welfare but also each coalition country’s moral welfare increases with the coalition size. Furthermore, each fringe country’s material welfare increases with the coalition size because its consumption benefits increase and the climate damages decrease with the coalition size. Finally, Finus et al. (2021a, p. 18) prove that any Stackelberg game is superadditive, i.e. \(mV_c(m)\ge (m-1)V_c(m-1)+V_f(m-1)\) , because \(e_c(m)\) maximizes the sum of m countries’ moral welfare, taking \(e_f(e_c(m))\) into account. Since each fringe country’s moral welfare increases with the coalition size, superadditivity implies that global material and moral welfare also increase with the coalition size. Footnote 22
The second bullet of the lemma reveals that each fringe country’s emissions decrease with the altruism parameter and that global material welfare increases with the altruism parameter as in the Nash game. Consequently, the relative global material and moral welfare \(W/W^>>=V/V^>>\) increase with the altruism parameter. Contrary to the Nash game, global emissions need not decrease with the altruism parameter. Finally, we prove in Appendix A.3.4 that the slope of the fringe countries’ aggregate reaction function and, thus, the leakage rate to the fringe countries \(|R'_f|\) increases in absolute terms with the altruism parameter for \(D'''\le 0\) and \(B'''=0\) as in the Nash game. The higher this leakage rate, the smaller ceteris paribus the coalition’s ambition and the greater ceteris paribus the coalition’s strategic advantage over the fringe in the Stackelberg game (Finus et al. 2021b). Footnote 23
Now we turn to the first stage of the Stackelberg game. First note that Proposition 4 implies that all coalitions with \(\tilde\le 1\) are externally unstable because joining this coalition then increases the respective country’s moral welfare from \(V_f\le V^>>_i\) to \(V_c>V^>>_i\) . Consequently, global emissions are smaller and each country’s moral welfare is greater at the stable Stackelberg equilibrium than at BAU, and each fringe country’s welfare is greater than each coalition country’s welfare. Together with Proposition 5, this gives Footnote 24 , Footnote 25
(Instability of small coalitions) Suppose \(B'''\ge 0\) and \(D'''\le 0\) . Then, all coalitions \(m\le >\) are externally unstable, and the coalition \(m=\left\lfloor >+1\right\rfloor \ge 2\) is internally stable.
The coalition \(m=\left\lfloor >+1\right\rfloor \ge 2\) is internally stable because leaving the coalition decreases the respective country’s moral welfare from \(V_c>V^>>_i\) to \(V_f\le V^>>_i\) . The lemma indicates that the coalition size increases with the threshold coalition \(>\) , which in turn tends to increase with the altruism parameter from Proposition 5. Via this mechanism, altruism could stabilise larger coalitions.
For the detailed stability analysis, we use specification (9). We constrain the parameter space to ensure non-negative emissions for all \(m\in [2,n]\) , which gives an upper bound for d similar to the Nash game. In particular, we formulate the following
This assumption is necessary and sufficient for non-negative emissions for all \(m\in [2,n]\) with \(\alpha =0\) . Footnote 26 In Appendix A.3.5, we then prove Footnote 27
Consider specification (9) with \(n\ge 7\) and \(d\le \bar>>\) .
Contrary to the Nash game, Proposition 6 reveals that altruism stabilises larger coalitions. However, the coalition never comprises more than six countries. More importantly, the coalition is always smaller than \(m=>+2\) . Since the Stackelberg equilibrium and BAU coincide for \(m=>\) , the emissions-reducing and welfare-enhancing effects of the coalition size from Lemma 2 are negligible. In fact, the small coalitions stem from constraining the parameter space to ensure non-negative emissions for \(m\in [2,n]\) , which gives an upper bound for d/b and, thus, for \(>\) . From Proposition 5, this upper bound increases with the altruism parameter, which is the driving force for larger coalitions with than without altruism.
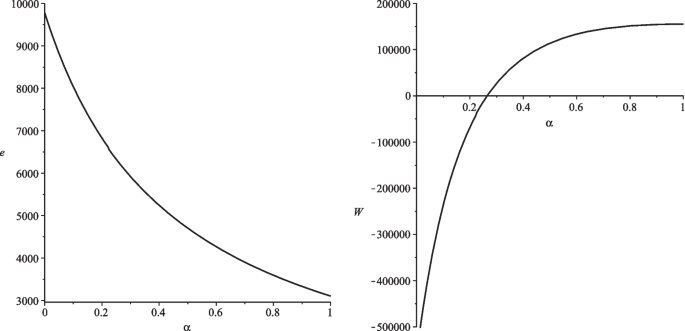
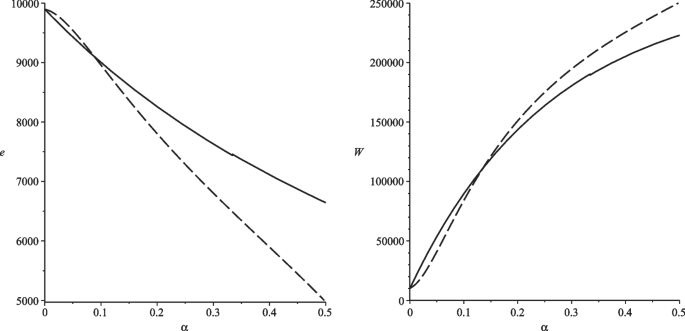
We use a numerical example to demonstrate there are economies in which the coalition is larger with than without altruism. Figure 3 depicts each coalition country’s minimal emissions Footnote 28 (left-hand side figure) and the internal stability condition (right-hand side figure) for \(m=3\) (solid curve) and for \(m=4\) (dashed curve) dependent on \(\alpha\) . In the numerical example, each coalition country’s emissions are positive for all \(m\in [2,n]\) . Furthermore, \(m=3\) becomes stable for \(\alpha \ge 0.223\) , and \(m=4\) becomes stable for \(\alpha \ge 0.839\) . Thus, there are economies in which the coalition is larger with than without altruism. Finally, Fig. 4 shows that global emissions decrease and global material welfare increases with the altruism parameter in the numerical example. Furthermore, as the coalition gets larger at \(\alpha =0.223\) and at \(\alpha =0.839\) , global emissions jump downwards and global material welfare jumps upwards, but these jumps are (almost) not visible.
The previous sections have shown that altruism affecting the membership decision and the policy decision leads to small (Proposition 2) or ineffective (Proposition 6) climate coalitions. By contrast, altruism affecting the membership decision only (van der Pol et al. 2012) can stabilise the grand coalition (Proposition 3). Footnote 29 Given that the effects of altruism on the formation of climate coalitions crucially depends on its modelling, this section discusses which realms of decision making might be influenced by social preferences in general. Footnote 30
We start by looking at what assumptions the literature on self-enforcing international environmental agreements with social preferences makes and how it justifies them. First, the literature incorporating inequality aversion (Lange and Vogt 2003; Lange 2006; Vogt 2016; Rogna and Vogt 2022) considers social preferences at both stages of the game and argues that governments interested in re-election must take (median) voters’ fairness preferences into account in national policy and international negotiations. Second, the literature incorporating reciprocal fairness (Grüning and Peters 2010; Nyborg 2018) also considers social preferences at both stages of the game. Footnote 31 Nyborg (2018, p. 707) argues that although groups may act differently than individuals, policy makers and treaty negotiators tend to be reciprocal when the general population is reciprocal, and tend to act reciprocally when the median voter is reciprocal. Third, the literature incorporating Kantian ethics (Eichner and Pethig 2022; Ulph and Ulph 2023) allows for different moral behaviour at the two stages of the game. Nevertheless, Eichner and Pethig (2022, pp. 18–19) argue that moral behaviour at just one stage of the game or different moral behaviour at the two stages of the game appears to be implausible, and Ulph and Ulph (2023, p. 12) “recognise that there is a strong argument that an agent should take the same moral stance to all decisions.” However, the latter argue that governments decide on coalition membership, while both governments and individuals decide on domestic emissions through public policy and private behaviour, respectively, such that the “decisions involve somewhat different agents”, which might explain different moral behaviour at the two stages of the game. Finally, van der Pol et al. (2012, p. 114) argue that “agents may hold different preferences when acting in different social situations, for example as consumers or as citizens.” They then distinguish between the decision about the technology employed and the domestic regulations adopted of a homo economicus with “personal well-being functions” (Nyborg 2000, p. 305), and the decision about the membership in the coalition of a homo politicus with “subjective social welfare functions” (Nyborg 2000, p. 305).
To sum up, most of the literature assumes that individual social preferences affect both stages of the game via the median voter (or because policy makers and treaty negotiators tend to have the same social preferences as the general population). On the other hand, taken together, van der Pol et al. (2012) and Ulph and Ulph (2023) provide good arguments that social preferences could be different at the two stages of the game: If there is a distinction between homo economicus and homo politicus and if homo economicus can influence domestic emissions, then social preferences might be more pronounced at the membership stage than at the policy stage. However, note that the cited literature (and the present paper) abstracts from individual decisions and assumes that countries or governments decide on both coalition membership and domestic emissions. In this case, all decisions are made by citizens rather than by consumers, and there should be no qualitative difference between social preferences at the two stages of the game.
However, strategic delegation could be another argument for different social preferences at different game stages. The literature on strategic delegation shows that strategic voters elect policy makers who care less about global public goods when policy makers bargain over their provision. Thereby, Buchholz et al. (2005) and Loeper (2017) assume that policy makers decide on the cooperative bargaining outcome and on the non-cooperative bargaining default (strong delegation), while Segendorff (1998) and Graziosi (2009) also consider policy makers deciding on the cooperative bargaining outcome but median voters deciding on the non-cooperative bargaining default (weak delegation), which leads to different preferences at different game stages. Footnote 32 Spycher and Winkler (2022) introduce strategic delegation into the standard two-stage game of self-enforcing international environmental agreements. They distinguish between weak delegation, i.e. elected policy makers decide on coalition membership but median voters decide on emissions policy, and strong delegation, i.e. elected policy makers decide at both stages of the game. While weak delegation does not increase coalition size but does increase global emissions, strong delegation can stabilise the grand coalition and thereby bring about the social optimum. These results suggest that strategic delegation can pay off. In this context, Lange and Schwirplies (2017) argue that there is indeed strategic delegation in climate policy because the social preferences of climate negotiators and the general population differ in that the former are more likely to support burden-sharing rules with low economic costs for their regions than the latter.
This section performs two model extensions. The first subsection shows that a small degree of community altruism can stabilise the grand coalition. The second subsection reveals that altruism can stabilise coalitions of two countries but tends to destabilise coalitions of three or more countries with linear climate damages and asymmetric countries. Footnote 33
In this subsection, we consider community altruism. In particular, we distinguish between out-group altruism \(\alpha\) and in-group altruism \(\beta >\alpha\) . The psychological literature has developed and tested two theories in particular for the preference of in-group members over out-group members (Balliet et al. 2014): The social identity theory assumes that individuals identify themselves with their memberships in social groups (Tajfel et al. 1979), while the theory of bounded generalized reciprocity assumes that groups contain individuals with cooperative reputations, which induces indirect reciprocity (Yamagishi and Kiyonari 1999). Cheikbossian (2021a) shows that in-group altruism is evolutionary stable, Cheikbossian (2021b) finds that a combination of in-group altruism and out-group altruism can be evolutionary stable, and Balliet et al. (2014) summarize the significant evidence for in-group altruism (and against out-group spite) in psychological experiments.
In the following, we first analyse community altruism in the Nash game then report the effects of community altruism in the Stackelberg game. In the Nash game of coalition formation, each fringe country does not belong to a group, such that its moral welfare (1) and its first-order condition (4) do not change. By contrast, each coalition country belongs to the climate coalition, such that its moral welfare becomes
Thus, community altruism ceteris paribus increases the weight of the coalition’s material welfare. Rearranging the corresponding first-order condition yields Footnote 34
$$\beginwhere the numerator reflects the altruistic preferences of the respective coalition country for all other countries’ climate damages, and the denominator reflects the altruistic preferences of all other coalition countries for the respective coalition country’s consumption benefits. Community altruism reduces the relative importance of the fringe countries’ climate damages, which ceteris paribus increases the coalition’s emissions. However, from (4) and (17), we infer
$$\beginConsequently, each fringe country’s emissions are still greater than each coalition country’s emissions. In Online Appendix B.1.1, we prove that the first bullet and the third bullet of Proposition 1 also hold with community altruism: Each coalition country consumes less than at BAU, which reduces global emissions and, thus, marginal climate damages, such that each fringe country consumes more than at BAU. Consequently, the material welfare of each fringe country is greater than that of each coalition country and greater than that at BAU. However, and in contrast to the case without community altruism, the moral welfare of each coalition country can be greater than that of each fringe country if the material welfare of each coalition country is positive, because then community altruism ceteris paribus increases the former but does not affect the latter. In particular, we have \(V_f-V_c=(1-\alpha )(W_f-W_c)-(\beta -\alpha )(m-1)W_c\) , which ceteris paribus decreases with the degree of community altruism and with the coalition size if \(W_c>0\) . This welfare effect of community altruism can reduce the free-rider incentives.
To analyse the policy effect of community altruism, we prove in Online Appendix B.1.1 Footnote 35
(Effects of community altruism on emissions and welfare)
Ceteris paribus, community altruism does not affect each fringe country’s consumption, see (4), but increases each coalition country’s consumption, see (17). Thus, \(e_c\) increases, which increases global emissions and, thus, marginal climate damages, such that \(e_f\) decreases. Consequently, each fringe country’s material welfare decreases, while the increase in each coalition country’s consumption benefits outweighs the increase in the climate damages, such that its material welfare increases. This policy effect of community altruism raises each coalition country’s moral welfare and reduces the difference between the moral welfare of each fringe country and each coalition country if \(W_c\ge 0\) . Furthermore, it reduces each fringe country’s moral welfare \(V_f=(1-\alpha )W_f+\alpha W\) if \(\alpha\) is sufficiently small, such that the decrease in \(W_f\) outweighs the potential increase in W.
Taken together, the sign of each coalition country’s material welfare plays an important role for the effects of community altruism on the free-rider incentives. This also becomes clear when we look at the (internal) stability condition of the grand coalition:
$$\begin
First note that the grand coalition maximizes global material welfare from \(V_c(n)=[1+\beta (n-1)]W_c(n)\) as in the case without community altruism. Now consider \(\beta =1\) . Then, \(V_c(n)\) is maximized global material welfare W(n), and \(V_f(n-1)\) is non-maximized global material welfare \(W(n-1)\) minus the coalition’s material welfare weighted by \(1-\alpha\) . Thus, the grand coalition is stable if \(W_c(n-1)\ge 0\) . By contrast, if \(W_c(n-1)W(n) if \(W_c(n-1)0\) holds with specification (9) when there is a sufficiently large number of countries ( \(n\ge 9\) ). Then, the emissions policy of one fringe country is relatively unimportant for the material welfare of many coalition countries. In this case, the grand coalition is stable for \(\beta =1\) .
Note that \(W_c(n)\) is always non-negative because the grand coalition could choose \(e_c=0\) and, thus, \(B(0)\ge 0\) and \(D(0)=0\) . Consequently, in-group altruism increases each country’s moral welfare in the grand coalition. Furthermore, it reduces each fringe country’s material welfare, but raises each coalition country’s material welfare with any other coalition, such that the effect on each fringe country’s moral welfare is in general ambiguous. However, in Online Appendix B.1.1 we prove that this effect is definitely negative if there is only one fringe country. Then, in-group altruism increases the emissions of so many coalition countries that the corresponding increase in climate damages and decrease in the fringe country’s consumption benefits outweigh the increase in the coalition country’s consumption benefits. To sum up, in-group altruism increases the stability of the grand coalition.
Finally, out-group altruism does not affect each country’s moral welfare in the grand coalition, but it reduces global emissions and increases global material welfare with any other coalition, see Lemma 1. Thus, it also tends to increase \(V_f(n-1)=W_f(n-1)+\alpha (n-1)W_c(n-1)\) if \(W_c(n-1)>0\) . Consequently, it can be shown that out-group altruism increases the fringe country’s moral welfare with specification (9) when there is a sufficiently large number of countries ( \(n\ge 10\) ). In this case, out-group altruism decreases the stability of the grand coalition. We prove our results in Online Appendix B.1.1 and summarize them in
(Stability of grand coalition with community altruism) Consider specification (9).
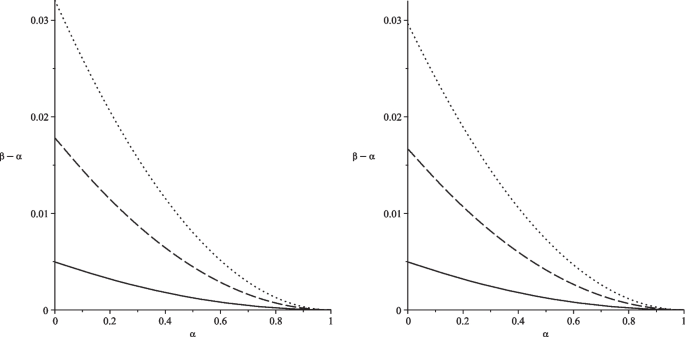
Thus, community altruism can stabilise the grand coalition and thereby bring about the social optimum. Figure 5 depicts thresholds of \(\beta -\alpha\) for the grand coalition to be stable dependent on \(\alpha\) in the Nash game (left-hand side figure) for different values of the climate damage parameter d. Footnote 36 When this parameter is small, emissions policy is determined mainly by marginal emissions benefits rather than marginal climate damages, so that the difference between the emissions and therefore the material welfare of each fringe country and each coalition country is small, which reduces free-rider incentives and stabilises the grand coalition. Figure 5 shows that the grand coalition can be stable even with a small difference between in-group altruism and out-group altruism of less than 0.03. Footnote 37 Note that community altruism does not change the grand coalition’s emissions policy, so its stabilizing effect relies on the worse emissions policy for the final fringe country (policy effect) and on the increased moral welfare of each coalition country for a given emissions policy (welfare effect). Footnote 38
Finally, we report the effects of community altruism in the Stackelberg game. Since the results are simply a combination of those in the Stackelberg game without community altruism and those in the Nash game with community altruism, we delegate the full analysis to Online Appendix B.1.2. First, there is a unique threshold coalition \(<\hat
In this subsection, we consider asymmetric countries in terms of consumption benefits \(B_i(e_i)\) and climate damages \(D_i(e)\) . With convex climate damages \(D''_i>0\) (or abatement benefits), the results of previous literature on coalition stability with asymmetric countries are based on numerical analyses (Barrett 1997; Botteon and Carraro 2001; McGinty 2007; Bakalova and Eyckmans 2019; McGinty 2020). In order to obtain analytical results, we thus rely on linear climate damages \(D''_i=0\) in this subsection. This implies that each fringe country has a dominant strategy, such that the Nash game and the Stackelberg game coincide. Furthermore, we focus on the case without transfers.
In such a framework with two types of countries, Fuentes-Albero and Rubio (2010) show that a coalition of at most three countries is stable if either climate damages or emissions benefits are symmetric. Pavlova and De Zeeuw (2013) confirm this result and show that the same holds if climate damages and emissions benefits are positively correlated. By contrast, if climate damages and abatement costs are negatively correlated, a coalition of all countries with low climate damages and two countries with high climate damages can be stable. Finus and McGinty (2019) extend this analysis by allowing for any type of countries. They show that the grand coalition can be stable if climate damages and abatement costs are negatively correlated.
Following van der Pol et al. (2012), we consider a unique altruism parameter to derive the general effects of altruism on the formation of climate coalitions. Furthermore, we abstract from community altruism to check the robustness of our main model with linear climate damages and asymmetric countries. With a unique altruism parameter and without community altruism, each country’s moral welfare function is still given by (1), and the global moral welfare function is still given by (2). Consequently, the socially optimal emissions always maximize global material welfare, and the individually optimal emissions maximize global material welfare if and only if \(\alpha =1\) . In Appendix A.1, we prove that global emissions decrease and global material welfare increases with the altruism parameter in the individually optimal solution as in the main model. Consequently, the relative global emissions \(e^>>/e^>>\) decrease and the relative global material and moral welfare \(W^>>/W^>>=V^>>/V^>>\) increase with the altruism parameter.
In the coalition formation game, each fringe country’s moral welfare is still given by (1), and the sum of the coalition countries’ moral welfare is still given by (3). Rearranging the corresponding first-order conditions yields